Ein wenig Mathematik muss sein:
- kleiner Exkurs in die Winkelfunktionen -
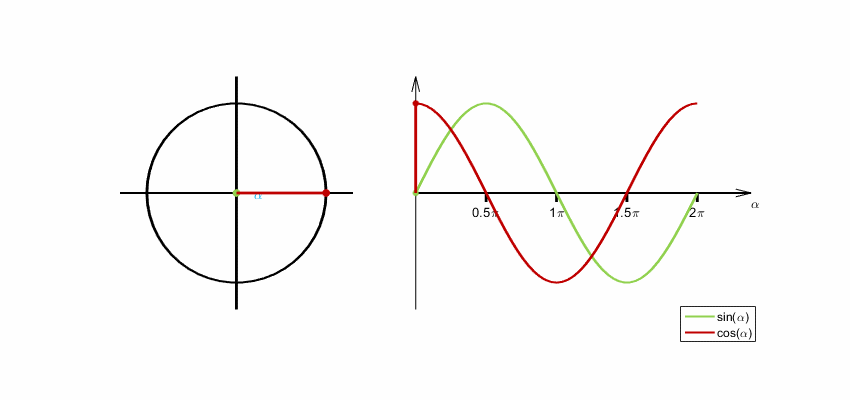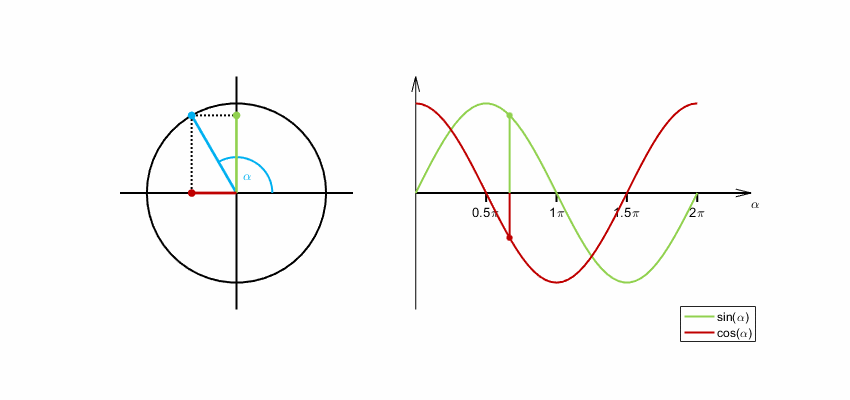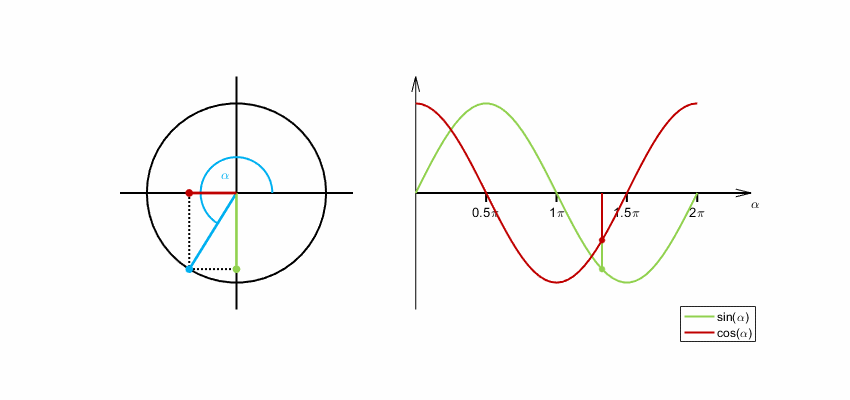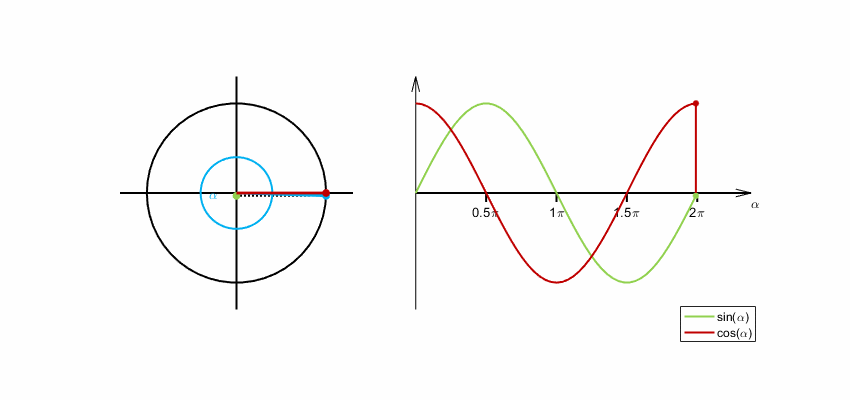
Bildbox 1 (klick hier)
Ein wenig Mathematik muss sein:
- kleiner Exkurs in die Winkelfunktionen -

![]()
Bildbox 1 (klick hier)
Hardware
- Rundes 1,28-Zoll-IPS-LCD-Display RP Pico 2040 oder
- Rundes 1,28-Zoll-IPS-LCD-Display RP Pico 2350
- USB-A zu USB-C Kabel
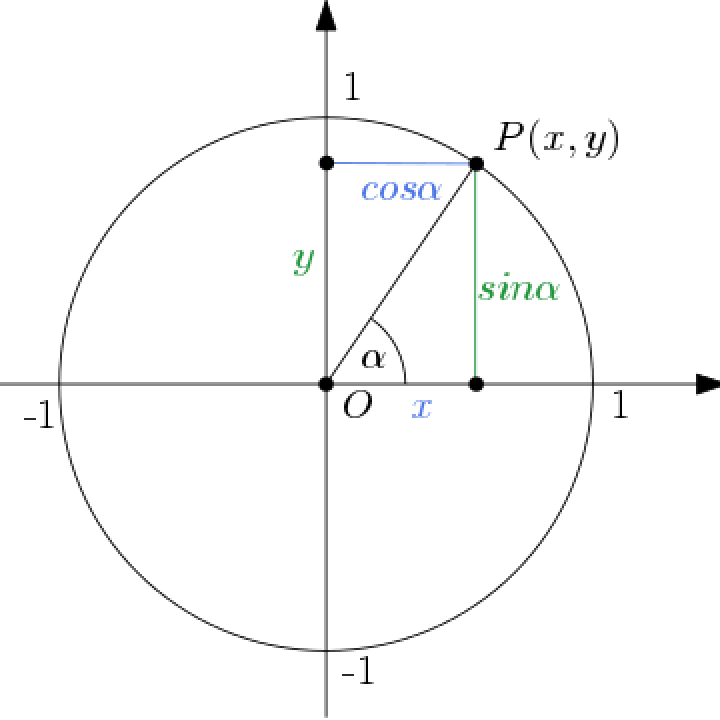
Unser Display ist rund. Deshalb kommt man z.B. bei der Darstellung von Punkten, Zeigern u.ä. nicht ohne die Winkelfunktionen Sinus und Cosinus
aus. Gehen wir kurz auf die Definitionen von Sinus und Cosinus ein.
Auf den beiden unteren Fotos wird das für die 'Sekundenpunkte', 'Minutenpunkte', 'Stundenpunkte' bzw. die Position der Zeigerspitzen genuzt.


Los gehts mit einem Beispiel
(Verwenden Sie als Bibliotheken im 'lib-Ordner' die selben, wie in der Anleitung 'verbesserte Analoguhr' hier .)
Das Display hat 240 x 240 Pixel. Der Mittelpunkt liegt also bei P(120/120), so dass wir als Koordinaten nachfolgend immer xpos = 120 und ypos = 120 nutzen.
Die jeweils neue x-Koordinate ergibt sich dann aus
Da 2*pi bekanntlich 360 Grad entsprechen, lassen sich mit pi/30 die 60 'Positionen' (360 / 180 * 30 = 60) darstellen. Mit der 100 wird in unserem Fall der Radius festgelegt. Hier nun das Beispielprogramm:
1 # SPDX-FileCopyrightText: 2023 Detlef Gebhardt, written for CircuitPython 2 # SPDX-FileCopyrightText: Copyright (c) 2023 Detlef Gebhardt 3 # 4 # SPDX-License-Identifier: GEBMEDIA 5 import time 6 import gc 7 import board 8 import busio 9 from busio import I2C 10 import displayio 11 import terminalio 12 import gc9a01 13 from adafruit_display_text import label 14 from adafruit_display_shapes.circle import Circle 15 import random 16 import math 17 import fourwire 18 # Release any resources currently in use for the displays 19 displayio.release_displays() 20 21 # Make the displayio SPI bus and the GC9A01 display 22 spi = busio.SPI(clock=board.GP10, MOSI=board.GP11) 23 display_bus = fourwire.FourWire(spi, command=board.GP8, chip_select=board.GP9, reset=board.GP12) 24 display = gc9a01.GC9A01(display_bus, width=240, height=240, backlight_pin=board.GP25) 25 26 # Make the display context 27 group1 = displayio.Group() 28 display.root_group = group1 29 30 width = 240 31 height = 240 32 xpos = 120 33 ypos = 120 34 radius = 120 35 i = 0 36 37# Make some circle: 38 circle = Circle(xpos, ypos, 120, fill=0xff0000, outline=0x000000) 39 group1.append(circle) 40 circle = Circle(xpos, ypos, 115, fill=0x000000, outline=0x000000) 41 group1.append(circle) 42 circle = Circle(xpos, ypos, 85, fill=0xffff00, outline=0xffff00) 43 group1.append(circle) 44 circle = Circle(xpos, ypos, 10, fill=0x0000ff, outline=0xffff00) 45 group1.append(circle) 46 47 while True: 48 for i in range (60): 49 xpos_neu = int(width/2 + 100*math.cos((i -15)*math.pi/30)) 50 delta_x = xpos_neu - xpos 51 xpos = xpos_neu 52 ypos_neu = int(height/2 + 100*math.sin((i -15)*math.pi/30)) 53 delta_y = ypos_neu - ypos 54 ypos = ypos_neu 55 circle.x = circle.x + delta_x 56 circle.y = circle.y + delta_y 57 time.sleep(0.05) 58 gc.collect() 59 #print(gc.mem_free())
Ein paar Erläuterungen. Die Programmzeilen 5 bis 28 entsprechen dem vorigen Beitrag zur Initialisierung des
Displays. Hinzu gekommen sind die Module 'from adafruit_display_shapes.circle import Circle' und
'import math', welche für die Kreisdarstellung und die mathematischen Berechnungen gebraucht
werden. In den Zeilen 37 bis 45 werden Kreise dargestellt, welche nacheinander das Display rot, dann mit kleinerem Durchmesser
schwarz und schließlich gelb einfärben. Zuletzt wird ein kleiner blauer Kreis als Punkt in dem schwarzen Ring
dargestellt. Sie sehen, dass die Syntax für den Kreis immer
circle = Circle(xpos, ypos, radius, fillcolor, outlinecolor)
ist. Es folgt die 'while' Schleife in Zeile 47. Dort wird in den Zeilen 56 und 57 eine Eigenschaft bei 'circle' genutzt, welche
mit 'circle.x' bzw. 'circle.y' die neue x und y Position des Mittelpunktes annehmen kann, ohne den Kreis neu definieren zu
müssen. Stattdessen wird in den Zeilen 49 bis 54 der neue geänderte Wert berechnet und als 'delta_x' und 'delta_y' zu
den Mittelpunktkoordinaten addiert. Dass hat den riesigen Vorteil, dass kein zusätzlicher Speicher belegt wird, denn dann
würde ganz schnell ein 'MemoryError' das Programm beenden.
Ich habe das Ganze in eine 'for i in range (60)' Schleife gepackt, deshalb steht in Zeile 49 und 52 beim Sinus bzw. Cosinus das 'i'.
Die subtrahierte 15 hat ihren Sinn, weil ich das Display bei der Initialisierung um 90 Grad gedreht habe (siehe Zeile 24) und die
Bewegung oben beginnen soll. Experimentieren Sie mit dem Beispiel und demnächst geht es weiter.
Zuvor gibt es aber noch eine kleine Zugabe. Probieren Sie das folgende Programm aus.
Zum Zeitpunkt als diese Seite erstellt wurde, war der Treiber für den ACC-Sensor unter CircuitPython noch
nicht fertig. Deshalb wurde mit Hilfe der Zufallsfunktion 'random' ein 'wert = random.randint(min,max)' als ganzzahliger
Zufallswert zwischen 'min' und 'max' erzeugt. Dieser wurde für die x- und y-Koordinaten verwendet, so dass der Punkt hin- und
hersprang, bis er den weißen Punkt traf.
1 # SPDX-FileCopyrightText: 2023 Detlef Gebhardt, written for CircuitPython 2 # SPDX-FileCopyrightText: Copyright (c) 2023 Detlef Gebhardt 3 # 4 # SPDX-License-Identifier: GEBMEDIA 5 import time 6 import gc 7 import board 8 import busio 9 from busio import I2C 10 import displayio 11 import terminalio 12 import gc9a01 13 import my_qmi8658 14 from adafruit_display_text import label 15 from adafruit_display_shapes.circle import Circle 16 import random 17 import fourwire 18 # Release any resources currently in use for the displays 19 displayio.release_displays() 20 21 # Make the displayio SPI bus and the GC9A01 display 22 spi = busio.SPI(clock=board.GP10, MOSI=board.GP11) 23 display_bus = fourwire.FourWire(spi, command=board.GP8, chip_select=board.GP9, reset=board.GP12) 24 display = gc9a01.GC9A01(display_bus, width=240, height=240, backlight_pin=board.GP25) 25 26 # Make the display context 27 group1 = displayio.Group() 28 display.root_group = group1 29 30 # acc initialisieren 31 sensor=my_qmi8658.QMI8658() 32 33 width = 240 34 height = 240 35 xpos = 120 36 ypos = 120 37 radius = 120 38 xpos_neu = 0 39 ypos_neu = 0 40 41 # Make some circle: 42 circle = Circle(xpos, ypos, 120, fill=0xff0000, outline=0x000000) 43 group1.append(circle) 44 circle = Circle(xpos, ypos, 110, fill=0x000000, outline=0x000000) 45 group1.append(circle) 46 circle_m = Circle(xpos, ypos, 16, fill=0xffffff, outline=0x000000) 47 group1.append(circle_m) 48 circle_p = Circle(xpos, ypos, 10, fill=0x0000ff, outline=0xffff00) 49 group1.append(circle_p) 50 51 while True: 52 #read QMI8658 53 val=sensor.Read_XYZ() 54 # Display wird rel. zur x-Achse bewegt 55 wert_x = (100)*val[0] 56 # Display wird rel. zur y-Achse bewegt 57 wert_y = (50)*val[1] 58 # x-Werte 59 ## Ausschlag nach rechts 60 if wert_x < 0 and wert_x >= -10: 61 x = +5 62 # Ausschlag nach links 63 if wert_x >= 0 and wert_x < 10: 64 x = -5 65 # y-Werte 66 ## Ausschlag nach oben 67 if wert_y >= 0 and wert_y < 10: 68 y = -5 69 # Ausschlag nach unten 70 if wert_y < 0 and wert_y >= -10: 71 y = +5 72 circle_p.x = circle_p.x + x 73 circle_p.y = circle_p.y + y 74 display.refresh() 75 time.sleep(0.05) 76 gc.collect() 77 #print(gc.mem_free())
Dies ist jetzt insofern anders, dass der Sensor genutzt wird. Wenn sich das Display bewegt, werden die sich ändernten Werte
genutzt, um die Koordinaten des 'Punktes' zu beeinflussen.
Erinnert Sie das auch an ein Spiel aus der Kindheit, bei dem eine Kugel in einer kleinen Dose in ein Loch jongliert werden
mußte. In unserem Fall steckt die Idee dahinter, dass dies unter Nutzung des Beschleunigungssensors, über den unser
rundes Display verfügt, gemacht wird. Wenn Sie Lust haben, können Sie das kleine Gimmick gerne noch erweitern.
Viel Spass und Erfolg beim Ausprobieren.
Viel Spass und Erfolg beim Ausprobieren.